Art From Chaos
Table Of Contents
Making art is hard. Drawing pictures is tedious. With programming, however, we can automate things. The point of automation is to reduce the amount of manual labor. So let’s mix evolution, DNA, and programming together to make art that makes itself. Pictures that draw themselves.
Concepts and definitions
Before we dive deep into making art, we need to understand some important concepts – first things first. Automatic art1, at its core, uses generic algorithms. Wikipedia has a really nice page about them, if you’d like to read it. However for the sake of the article this is enough:
A Genetic Algorithm is an algorithm inspired by the process of natural selection used to find solutions for optimization problems. It has three main parts:
- Mutation - during which specimens are randomly changed,
- Scoring - during which specimens are ranked by their “ability to adapt to their environment”,
- Crossing - during which one or more specimens are mixed together to produce a new member.
OK. 👌
With these terms out of the way, let’s try to understand how exactly it works. Imagine we need to find a solution for a problem. It can be anything, like finding optimal timetable for a university class. Firstly, we need to encode a solution as a series of bytes (their Genetic representation, if you will). Once we have that we can clone the encoded representation to create a generation.
Each member of the generation will be randomly mutated and then scored based on how well they fit in our
constrains set. For example: we might want to have a timetable which leaves just enough break time to eat a quick lunch,
but not too much, so that we can go home earlier. This (and similar constrains) might be used to evaluate the value of
our new mutated timetable. With each specimen evaluated we leave a few of the best and discard the rest 💀.
The last step is to mix our special timetables to create new ones to fill the generation again.
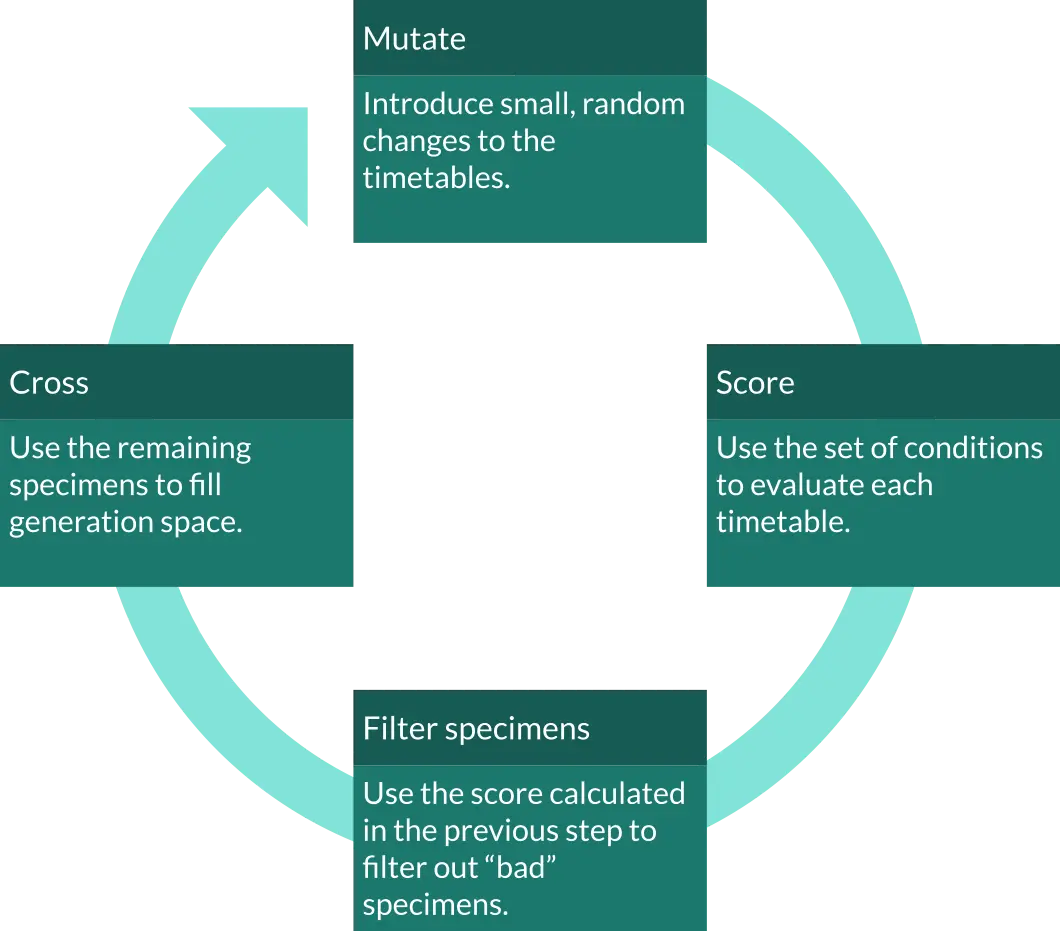
To mutate, to score, to kill, to breed, to continue the cycle of life. It might sound simple, but in reality it is shockingly efficient in searching the solution space.
Art from evolution
Alright. Now with the theory out of the way, let’s conceptualize a program for generating automatic art. Probably it’s a good moment to explain the clickbaity summary at the top of this article: the pictures will not draw themselves, the goal is to make a program which will generate art automatically. It’s going to be an iterative solution where each cycle is parametrized by the results of its predecessor.
Step 0: Initialization
Before we do anything towards evolution we need to prepare a generation first. So what’s our generation size? Let’s see if Wikipedia has something insightful to say:
The population size depends on the nature of the problem, but typically contains several hundreds or thousands of possible solutions.
~ Genetic algorithm @ Wikipedia
Well, that’s really not the most helpful answer. 😐
It really boils down to this: the more specimen we have, the more memory the program requires and more CPU time to
process each generation. On the other hand, the more specimen a generation have, the wider portion of solution space it
can search. Whatever the generation size will be, we need to have a prototype - a specimen, which cloned will fill the
generation. Since we’re dealing with art here, a tabula rasa should be a
fitting choice.
Step 1: Mutation
Mutation method greatly affects the end result, so it’s imperative to select a right one. Mutation algorithms are usually stateless, meaning modification of each specimen does not affect any other. In each iteration the mutator will introduce a small change into specimens’ genetic representation. On images it can be, for example: changing random pixels. This works, but the final image looks too detailed (in a bad way).
Now, the changes does not technically need to be small per se, however applying too big changes might result in overriding a portion of the genome that was making this particular specimen a good candidate, thus resulting in loosing progress achieved by previous generations.
If you’d google “generating images with genetic algorithm”, you’d find that most projects on the subject use geometric shapes when applying mutation. Simple onces, like circles, rectangles, and triangles are a good choice. From these it’s rectangles, that can be the most easily represented in code. Having said that let’s see how a single specimen might change over a few first iterations.
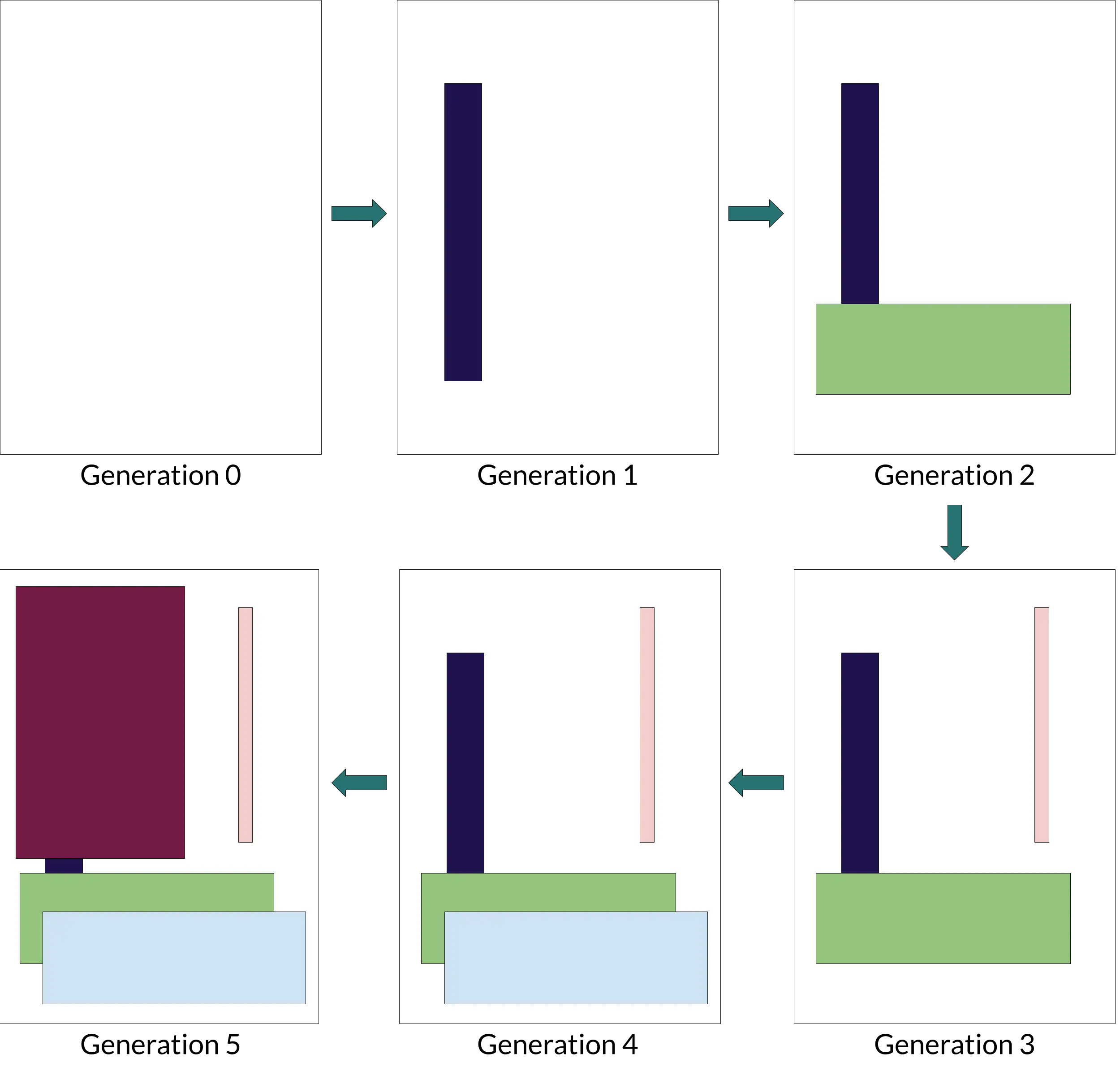
An exemplar of a 6-generation mutation process. Starting with generation 0 - no mutation applied, till generation 5 - five mutations applied.
Each of the rectangles on that picture represents a random mutation applied onto the image, meaning that all information needed to unambiguously identify a rectangle (width, height, coordinates of one of the corners, and its color) have been randomly generated.
The above illustrates the risk of allowing mutations which are not constrained by their impact: the mutation introduced in 1st step has been almost fully overwritten after 5 mutations. Don’t get me wrong, the result might be beneficial, but overall we want to utilize genome that have evolved in past generations, not to discard it completely.
Step 2: Scoring
Implementing scoring function can be tricky. Basically we need to have a way of mapping each specimen into an integer value. Then with values for all specimens we can calculate a threshold and filter out all images above it. The genetic algorithm does not provide to us any way of determining whether a mutation has been beneficial; that is strictly depends on the implementation. So let’s talk about what it is exactly we’d like to achieve here.
The idea behind generating images through evolution is that we have an ideal to which we’re aiming to get as close as possible. An original image, from which will derive a collection of images similar to it, each mutated and scored multiple times. A scoring function could calculate a difference between the original image and the one being currently scored:
$$ f(O, S) = \sum_{i=0}^n | O_n - S_n | \tag{1} $$
Both O and S refer to a collection of pixels representing the original image and the current specimen respectively,
thus allowing us to index their pixels and calculate a difference between them. This, on its own, isn’t the most helpful
piece of advice, as it glides over the fact that we a calculating a difference of pixels not numbers, we cannot do
arithmetics on them. To fix that we need to be a bit more clever here.
We can utilize the fact that pixels are just color, usually represented in RGB notation. Each color in the RGB color space is represented by three numbers from 0 to 255 (each encoding the amount of red, green, and blue). Numbers on their own don’t have any meaning, its the context that makes them colors, points, or geometric shapes. If we’d interpret these three numbers as coordinates in three-dimensional space, then they would become points. In that case, the difference between two points can be implemented as the distance between then:
$$ d(A, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} $$
Alright 👌. The final thought: this formula calculates the difference between two points in space, but we don’t really need the distance, just an indication of how similar the two pixels are. Since calculating a square root on computers is expensive, we can remove that bit and we’re left with:
$$ g(A, B) = (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 \tag{2} $$
By combining (1) and (2) together we get:
$$ f(O, S) = \sum_{i=0}^n | (r_2 - r_1)^2 + (g_2 - g_1)^2 + (b_2 - b_1)^2 | $$
That was a bit more mathsy that I’ve initially anticipated ◕_◕.
Step 3: Crossing
In the last step the algorithm has to fill up almost emptied generation. This step, quoting Wikipedia, it’s:
[…] a genetic operator used to combine the genetic information of two parents to generate new offspring. […] Solutions can also be generated by cloning an existing solution, which is analogous to asexual reproduction.
~ Crossover (genetic algorithm)
There are several ways we can make it work, from naive ones:
- create an exact copy of one of the remaining images,
- create a mutated copy of one of the remaining images,
- split image into two halves and fill it with a respective half from one of the two parents,
to more sophisticated ones:
- for each pixel pair taken from two parents calculate an arithmetic average and use it to construct a new pixel,
- for each pixel pair taken from two parents calculate an weighted average and use it to construct a new pixel.
The methods mentioned above differ in their complexity, but more importantly, in how fitting specimens they create. It’s worth to mention that in opposition to the previous two steps, this one isn’t strictly mandatory. The algorithm will still work without it and the generated images will look acceptable. With crossing, however the algorithm generates more fitting specimens, relative to a one without the 3rd step, in the same number of generations.
We will take a look at several of crossing methods mentioned above and we will plot scores of their specimens as a function of generation number, to see how well they perform. 📈
Next steps
This is the first article from a series about generating art through genetic algorithms. In the next articles (coming up soon-ish) we’ll turn those ideas into Rust code and after that we’ll finally make art that makes itself.

Photo by Brett Jordan on Unsplash
See you around!
🌊
Term coined by me. If you want to read more about art generated by algorithms you should probably look for Algorithmic art. ↩︎
Interested in my work?
Consider subscribing to the RSS Feed or joining my mailing list: madebyme-notifications on Google Groups .
Disclaimer: Only group owner (i.e. me) can view e-mail addresses of group members. I will not share your e-mail with any third-parties — it will be used exclusively to notify you about new blog posts.